Deep Learning: Introduction

Introduction

深度学习三步骤：定义网络、损失函数、优化

前馈神经网络

神经元

神经网络

全连接层

优化

卷积神经网络

全连接的前馈神经网络参数较多，需要较多样本学习；且很难提取局部不变性特征（过拟合）。

引入卷积神经网络，也是一种前馈神经网络，结构特性：局部连接、权重共享、空间或时间上的次采样

卷积

常用于计算信号的延迟积累

时刻t收到的信号$y_t$（卷积输出）为当前时刻产生的信息和以前时刻延迟的信息（输入信号序列）叠加：

$$y_t=\sum_{k=1}^Kw_kx_{t-k+1}$$

$w_k$称为滤波器或卷积核。

假设input信号序列长度为N，卷积核长度为K，则输出卷积信号长度为N-K+1.

卷积作用

• 近似微分：例：$[-\frac{1}{2},0,\frac{1}{2}]$近似一阶；$[1,-2,1]$近似二阶
• 低通滤波/高通滤波：例：$w=[\frac{1}{3},\frac{1}{3},\frac{1}{3}]$检测信号序列中的低频信息（变换缓慢，如均值）；$w=[1,-2,1]$检测信号序列中的高频信息（变化较快，如二阶导）

卷积扩展

• 滑动步长S：增加步长减少信号输出长度
• 零填充P：往信号输入两端补充P个0

根据卷积结果长度可以分为三类：

• 窄卷积：S=1，P=0.输出长度为M-K+1 早期文献默认
• 宽卷积：S=1，P=K-1.输出长度为M+K-1
• 等宽卷积：S=1，P=(K-1)/2.输出长度为M 目前文献默认

二维卷积

应用于图像处理等二维矩阵形式信息序列

定义一个输入信息$X$和滤波器$W$的二维卷积为$Y=W*X$，其中

$$y_{ij}=\sum_{u=1}^U\sum_{v=1}^Vw_{uv}x_{i-u+1,j-v+1}$$

同样有步长S和零填充P供选择。

作用：作为特征提取器

应用到神经网络中，希望自动学习这个卷积核$W$，用以提取特征。

神经网络

用卷积层代替全连接层。

参数数量大大降低，只有卷积核数量个。

互相关

计算卷积需要进行卷积核翻转，比较麻烦，但我们的目的其实是提取特征，因此翻转是不必要的。修改为互相关形式：

$$y_{ij}=\sum_{u=1}^U\sum_{v=1}^Vw_{ij}x_{i+u-1,j+v-1}$$

之后除非特别说明，一般都为互相关。

多个卷积核

使用多个卷积核，得到多个特征映射(depth)，并将其拼接起来作为输出。

例如某卷积层：

• 输入：D个特征映射$M\times N\times D$
• 输出：P个特征映射$M’\times N’\times P$

卷积层的映射关系

$$Z^P=W^P\otimes X+b^P=\sum_{d=1}^DW^{P,d}\otimes X^d+b^P,\\ Y^P=f(Z^P)$$

可以将P个输出的特征映射看为输入的D个特征映射的全连接！

卷积层结构：

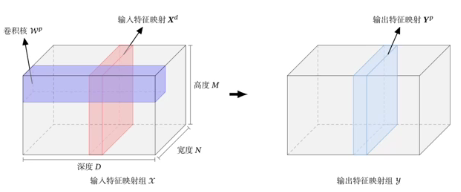
池化层（汇聚层）

卷积层可以显著减少连接个数（前馈神经网络是每一个输入信号有一个单独权重，得到总加权和，卷积神经网络是只有少数权重滑动加权，得到多个加权和），但是每个特征映射的神经元个数并没有显著减少（M-K+1）。

因此使用汇聚，将大的特征映射划分为几个小的特征映射，从每个小块中提取出一个代表元素。如：最大汇聚、平均汇聚、max-in-time(取每个depth最大的元素，好处是控制输出维数，只和卷积核的数量相关）。

可以看做特殊的卷积层

池化层结构：

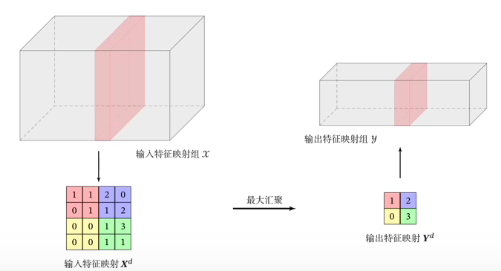
卷积网络结构

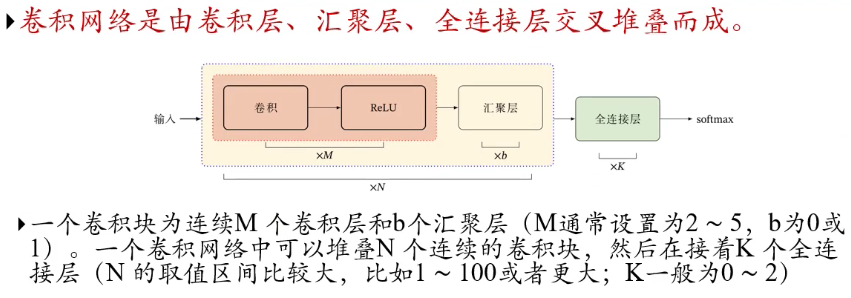
其他卷积网络

空洞卷积

增加输出单元的感受野的方法：

• 增加卷积核的大小
• 增加层数
• 在卷积之前进行汇聚操作（但会丢失部分信息）
• 空洞卷积：通过给卷积增加“空洞”来变相地增加其大小

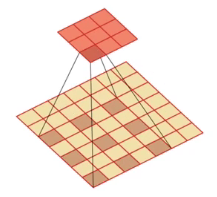
转置卷积/微步卷积

一般的卷积是高维映射为低维，该卷积将低维特征映射到高维特征。

思想就是将步长S调为小于1的值，方法为在元素之间以及矩阵周围插入适量的空格。

残差网络

问题：在深度网络中，使用一个非线性单元去逼近目标函数，会发现当目标函数为线性函数时，效果非常差。

解决方法：将目标函数拆分为两部分：恒等函数和禅茶函数：

$$h(x)=\underbrace{x}_{恒等函数}+\underbrace{(h(x)-x)}_{残差函数}$$

给非线性的卷积层（$h(x)-x$）添加直连边(shortcut connection)的方式来提高信息的传播效率。

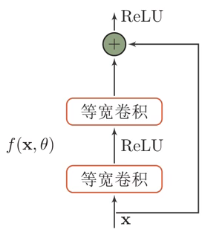
好处：当卷积函数的导数比较小时，加了一个x相当于加了偏置1，使得不会出现链式法则梯度消失的情况。

循环神经网络

不同于前两种，该网络信息可以反向传递。

当信号序列与时间相关时，有时候t时刻的输出不仅和t时刻的输入相关，还会和前面时间的输入、输出相关，但在前馈网络中，假设每次输入都是独立的，也即每次网络的输出只依赖于当前的输入。如何给网络增加记忆能力，处理任意长度的时序数据？：

时延神经网络

建立额外的延时单元，用以储存网络的历史信息（输入、输出、隐状态……）

$$h_t^{(l)}=f(h_{t}^{l-1},h_{t-1}^{l-1},\cdots,h_{t-K}^{l-1})$$

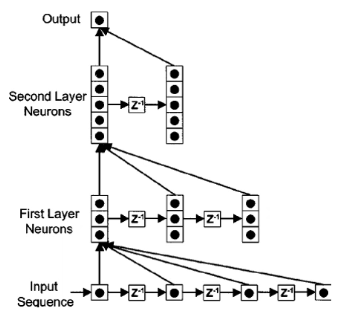
有外部输入的非线性自回归模型

自回归模型的加强版

自回归模型：一类时间序列模型，$y_t=w_0+\sum_{k=1}^Kw_ky_{t-k}+\epsilon_t$，其中$\epsilon_t\sim N(0,\sigma^2)$为噪声

有外部输入的非线性自回归模型：

$$y_t=f(x_t,x_{t-1},\cdots x_{t-K_x},y_{t-1},y_{t-2},\cdots,y_{t-K_y})$$

其中$f(\cdot)$是一个非线性函数 可以是前馈神经网络

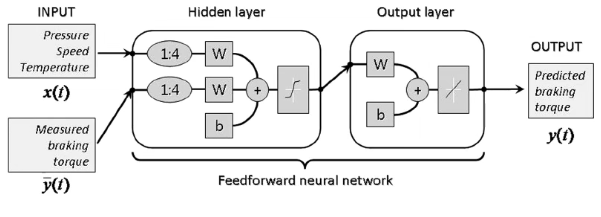
循环神经网络

使用带自反馈的神经元：$h_t=f(h_{t-1},x_t)$

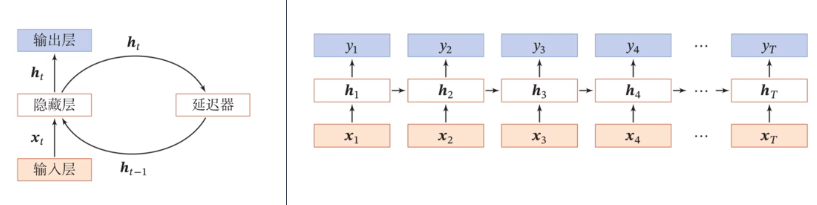
简单循环网络（SRN）

$$h_t=f(Uh_{t-1}+Wx_t+b)$$

由循环神经网络的通用近似定理可知，一个完全连接的循环网络是任何非线性动力系统的近似器。

图灵完备：所有的图灵机都可以被一个由使用Sigmoid型激活函数的神经元构成的全连接循环网络来进行模拟。

根据图灵完备，一个完全连接的循环神经网络可以近似解决所有可计算问题。

参数学习

以SRN为例，记$L=\sum_{i=1}^TL_t$为损失函数，则有

$$z_t=Uh_{t-1}+Wx_{t}+b\\ h_t=f(z_t)$$

根据以上两条公式，可推得（注意，基于寻欢神经网络的特性，$z_t$不止和$h_{t-1}$有关，事实上，是和所有$t-1$之前的$h$有关，求导时要注意）：

$$\frac{\partial L}{\partial U}=\sum_{t=1}^T\frac{\partial L_t}{\partial U}=\sum_{t=1}^T\sum_{k=1}^t\frac{\partial L_t}{\partial z_k}h_{t-1}^T=\sum_{t=1}^T\sum_{k=1}^t\delta_{t,k}h_{t-1}^T$$

P47 7:00